Jan 07
Une séquence d’enseignement-apprentissage est un regroupement logique d’éléments ciblés 
par les enseignantes et les enseignants que les élèves doivent apprendre dans une matière scolaire donnée. Généralement, l’enseignement-apprentissage de ces éléments ciblés dure environ sept semaines.1
Nov 27
Évaluer la compétence: RÉSOUDRE DES SITUATIONS-PROBLÈMES
Assurément, vous vous préparez à exercer votre jugement professionnel sur le développement des compétences avec le bulletin qui arrivera assez vite après le congé des Fêtes. Voici une question souvent posée: “Janvier, n’est-ce pas trop tôt pour évaluer la compétence à résoudre?” Comme le mentionne l’Info-Math du 27 octobre, les preuves d’apprentissages peuvent être observées grâce à plusieurs formes de situations.
Nov 10
Il existe deux grands enjeux de transition primaire/secondaire:
– Le vocabulaire mathématique
– Les représentations mathématiques
À ces deux enjeux s’joutent différents concepts ou aspects de la compétence: nombres entiers et décimaux, fractions, égalité suite et généralisation, estimation, rigueur, résolution de situations-problèmes, raisonnement et communication.
En observant les résultats (lien ci-bas), que peut-on conclure? Que peut-on proposer?
Arrimage primaire secondaire questionnaire mathématique
***************************
Collaboration interordres
L’équipe de Claudia Corriveau, Université Laval, s’est intéressée au travail de collaboration interordres. Le projet est présenté sur la site de l’ARIM (Actions et Rapprochements Interordres en Mathématiques).
Selon la recherche de madame Corriveau, quelles sont les conditions favorables pour initier cette collaboration interordres?
Établir un climat de confiance : il faut un temps d’apprivoisement. Les enseignants et les
enseignantes de différents ordres ont peu l’habitude de travailler ensemble.
Conscience du niveau de profondeur des discussions : cet aspect apparait particulièrement
important pour entrer dans une véritable collaboration. Nous voulons éviter les discussions
complaisantes et superficielles. L’objectif de la collaboration est ailleurs, les idées contraires,
la négociation et la profondeur de la réflexion sont nécessaires. Ce niveau de profondeur
doit être favorisé et à notre avis, par le rôle d’une tierce personne.
Participation démocratique : un dispositif de collaboration doit nécessairement être bien
organisé, certaines balises doivent être clairement définies. Il importe aussi de faire preuve
de souplesse et de penser les marges de manœuvre pour que ceux qui participent puissent
s’engager et avoir un droit de regard sur les objectifs à poursuivre.
Partage du leadership : nous avons identifié le rôle d’enseignants et d’enseignantes leaders
comme essentiel pour impliquer directement les enseignants et les enseignantes qui, dans
la recherche, ont pu démontrer leur aisance à livrer leur pratique, mais aussi qui ont pu
formuler comment des changements de pratique s’étaient opérés à travers leurs
expériences dans la collaboration interordre. Nous avons mis en évidence certains points
d’attention (terme emprunté à Desgagné, 1994) chez les enseignants et enseignantes
leaders (leadership, disposé à prendre des risques, aisance à communiquer, légitimité, etc.).
Résumé du rapport de recherche de madame Corriveau
Voir également: Arrimage intercycles et interordres.
Nov 09
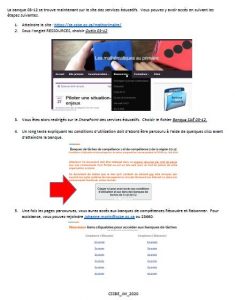Vous aviez l’habitude de retrouver la banque de situations-problèmes en passant par le bureau virtuel? Les banques développées par l’équipe régionale 03-12 et par le Récit Mathématique, Science et Technologie se retrouvent maintenant ici, sous l’onglet RESSOURCES. Pour vous aider à atteindre les SAÉ de l’équipe régionale 03-12, vous pouvez cliquer sur ce lien et consulter une procédure. Procédure Banque 03-12_nov2020
Nov 05
Oct 26
Il peut être intéressant de considérer l’écriture comme une occasion de résoudre des problèmes. En y réfléchissant, quels liens pourraient être établis entre écriture et résolution? Qu’en pensent les élèves?
Oct 21
Avant de commencer: Apprentissage à prioriser à l’enseignement primaire pour l’année 2021-2022 en contexte pandémique. (Ministère, août 2021, p. 16 à 21 )
**************************
Ces schémas synthèses présentent sous la forme d’un napperon les savoirs de la Progression des apprentissages. Au coeur, le sens du nombre qu’on développe tout au long des cycles pour assurer une compréhension empreinte de flexibilité et de fluidité. Les routines contribuent à cet objectif de même que les contextes authentiques de compétences résoudre et raisonner.
L’élaboration d’un aide-mémoire, seul document que les élèves pourront utiliser lors de l’épreuve du ministère en juin 2022, construit lors de séquences d’apprentissage contribue à développer la compréhension des concepts et processus mathématiques.
Oct 07
En mathématique, la représentation de l’information de façon visuelle est une compétence qui ne vient pas naturellement aux élèves; ils doivent l’acquérir et la perfectionner par la pratique. 1
Compétence à résoudre des situations problèmes
Les grilles descriptives pour l’évaluation des compétences mathématiques précisent certains éléments qu’il est nécessaire de se rappeler.
À la fin du premier cycle, l’élève interprète ou produit un message (oral ou écrit) tels un énoncé, un processus, une solution, en utilisant un langage mathématique élémentaire
et en faisant appel à au moins un mode de représentation : objets, dessins, tableaux, diagrammes, symboles ou mots.
Sep 30
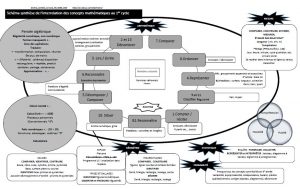
L’Info-Math 20-21 vous parvient tout au long de l’année pour vous entretenir de différents sujets mathématiques: des propositions, des pistes de réflexion, des ressources intéressantes, etc.
| L | M | M | J | V | S | D |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | |
© 2024 Les mathématiques au primaire.
Construit avec par Thèmes Graphene.
