Le saucissonnage qui tue le sens: un mot de madame Stella Baruk: ICI
1. Qu’est-ce qu’un bon problème?
Les situations-problèmes proposées à l’élèves dans le cadre de l’enseignement-apprentissage de la mathématique devraient faire l’objet d’une analyse à priori. Selon Charnay (2003), un bon problème doit permettre d’atteindre la zone proximale de la majorité des élèves. L’enseignant doit donc documenter son choix en émettant des hypothèses sur:
- les démarches, les stratégies et les procédures que les élèves utiliseront;
- les obstacles qu’il rencontreront et les erreurs que ceux-ci engendreront;
- l’organisation pédagogique qui favorisera l’apprentissage dans la classe;
- les interventions à mettre en place qui favoriseront l’apprentissage.
Les caractéristiques d’un problème selon le Référentiel d’intervention en mathématique (RIM, 2019) :
- il est formulé clairement sous forme d’un énoncé écrit, oral ou même illustré, de façon à être compris par tous les élèves;
- il est énoncé de façon à ne pas induire une stratégie de résolution ou l’emploi d’un algorithme en particulier;
- il éveille la curiosité et maintient l’intérêt des élèves;
- il incite à la réflexion et aux échanges mathématiques;
- il est à la portée de tous les élèves tout en leur offrant un défi;
- il se prête à l’utilisation d’une variété de stratégies de résolution;
- il fait appel au vécu des élèves;
- il donne lieu à une ou plusieurs réponses correctes.
 Grille d’analyse a priori d’un bon problème
Grille d’analyse a priori d’un bon problème
**************************************
La résolution de problèmes permet aux élèves :
● d’apprendre des concepts mathématiques grâce à un contexte qui encourage l’acquisition et l’utilisation d’habiletés;
● d’améliorer leur raisonnement mathématique en explorant diverses idées mathématiques, en faisant des conjectures et en justifiant les résultats;
● d’établir des liens entre les divers concepts mathématiques;
● de représenter des idées mathématiques et de modeler des situations à l’aide de divers outils tels que du matériel concret, des dessins, des diagrammes, des nombres, des mots et des symboles;
● de s’engager dans diverses activités et de choisir les outils (matériel de manipulation, calculatrice, outils technologiques) et les stratégies de calcul appropriés;
● de réfléchir sur l’importance du questionnement dans le monde des mathématiques;
● de s’intéresser aux mathématiques et de se questionner sur leur utilisation dans le monde qui les entoure;
● de persévérer en affrontant de nouveaux défis;
● de formuler leurs propres explications et d’écouter celles des autres;
● de participer à des activités d’apprentissage ouvertes qui permettent l’utilisation de diverses stratégies de résolution;
● de développer des stratégies applicables à de nouvelles situations;
● de collaborer avec les autres pour élaborer de nouvelles stratégies.
(Référence : Guide d’enseignement efficace des mathématiques, de la maternelle à la 6e année, fascicule 2, page 6.)
2. Ce qu’en disent les documents ministériels
La présentation des compétences mathématiques du PFEQ précise que ces dernières se développent en étroite relation. La distinction entre les compétences Résoudre et Raisonner est essentiellement une question d’accent mis sur différentes facettes de l’exercice de la pensée mathématique où tout s’intègre.
******
Précisions apportées par le Document d’informations de l’épreuve obligatoire et le PFEQ.
Une situation-problème pour développer la compétence RÉSOUDRE
Une situation-problème de compétence Résoudre engage l’élève dans un processus dynamique impliquant anticipations et retours en arrière. Elle est caractérisée par les éléments suivants:
- données complètes (1er cycle), superflues, implicites ou manquantes;
- questions pratiques plus ou moins familières issues de situations réelles et réalistes ou purement mathématiques;
- démarche pour arriver à la solution non immédiatement évidente (au moins deux réponses possibles);
- consignes ne donnant pas d’indications sur la démarche à suivre ou les savoirs essentiels à exploiter;
- choix et combinaison non apprises d’un nombre significatif de concepts et de processus dont l’apprentissage figure au programme de mathématique (au moins deux champs mathématiques);
- obstacles à franchir (étapes et contraintes, au moins 2 étapes liées par le contexte ou les mathématiques);
- processus de questionnement;
- mise en place de différentes stratégies (stratégies de compréhension, d’organisation, de solution, de validation et de communication);
- utilisation du matériel de manipulation;
- l’élève peut avoir besoin d’interventions pour clarifier des aspects de la situation-problème;
- le premier des 3 critères d’évaluation, Manifester sa compréhension, demande de s’intéresser aux étapes, aux données et aux contraintes.
Une situation d’application pour développer la compétence RAISONNER
Raisonner, c’est organiser de façon logique un enchaînement de faits, d’idées ou de concepts pour établir des relations et arriver à une conclusion. Afin de mieux comprendre l’utilité des mathématiques, l’élève est invité à inventorier des processus et des outils mathématiques de la vie quotidienne et dans les autres disciplines. Une situation d’application devrait permettre à l’élève:
- de choisir et d’appliquer les concepts et processus mathématiques requis et de présenter une démarche qui rend explicite son raisonnement;
- de justifier une affirmation, de vérifier un résultat ou une démarche, de prendre position, de critiquer ou de convaincre à l’aide d’arguments mathématiques (Pondération par critères pour une situation d’application: 30, 50, 20 et de validation 30, 40, 30)
- d’ utiliser prioritairement du matériel de manipulation.
- d’être évalué en fonction de 3 critères dont l’Analyse de la situation d’application implique les éléments et les actions.
Les grilles descriptives utilisées pour l’évaluation des compétences Résoudre et Raisonner impliquent les différents types d’erreurs (mineure, conceptuelle, procédurale).
Bien que présent dans la grille descriptive pour l’évaluation de la compétence Raisonner, le concept-clé n’apparaît pas dans l’épreuve du ministère 2019.
*****
3. Réalité et fausse réalité
Selon Lucie Deblois, r ésoudre un problème dans la réalité ou en mathématiques n’amène pas les mêmes démarches puisque certaines contraintes sont ignorées en mathématiques. Des contenus mathématiques, bien qu’inscrits dans des situations concrètes, priveraient les élèves d’une véritable activité mathématique à cause de l’absence de réalité immédiate, ce que nous appelons « fausse réalité ». Une activité d’apparence géométrique comme calculer le périmètre d’une clôture est en fait une activité arithmétique et peut conduire les élèves à appliquer une formule sans pour autant sentir la nécessité de contrôler le résultat. En effet, les élèves ne poseront pas la clôture. En outre, poser cette clôture pourrait les inviter à privilégier d’autres procédures. Bien que la pose d’une clôture soit une activité de la vie courante, le contexte du problème donné aux élèves est fictif.
ésoudre un problème dans la réalité ou en mathématiques n’amène pas les mêmes démarches puisque certaines contraintes sont ignorées en mathématiques. Des contenus mathématiques, bien qu’inscrits dans des situations concrètes, priveraient les élèves d’une véritable activité mathématique à cause de l’absence de réalité immédiate, ce que nous appelons « fausse réalité ». Une activité d’apparence géométrique comme calculer le périmètre d’une clôture est en fait une activité arithmétique et peut conduire les élèves à appliquer une formule sans pour autant sentir la nécessité de contrôler le résultat. En effet, les élèves ne poseront pas la clôture. En outre, poser cette clôture pourrait les inviter à privilégier d’autres procédures. Bien que la pose d’une clôture soit une activité de la vie courante, le contexte du problème donné aux élèves est fictif.
******
4. Les trois intentions de la résolution de problèmes (RIM, 2019)
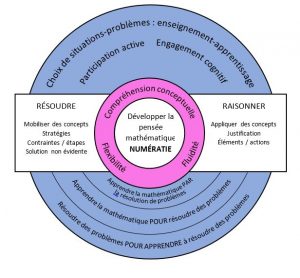
Apprendre la mathématique PAR
|
Apprendre la mathématique POUR résoudre des problèmesMobilisation et application des concepts et processus en situations contextualisées Consolidation la compréhension
|
Résoudre
|
Apprendre la mathématique PAR la résolution de problèmes
Selon Charnay (2005) les situations-problèmes choisies pour permettre l’apprentissage PAR la résolution de problèmes sont « auto-validantes ». C’est-à-dire qu’au terme de sa procédure, l’enfant peut se rendre compte s’il a réussi ou non.
Pour comprendre cette idée de rétroaction intrinsèque, le RIM propose l’exemple suivant vécu avec des élèves du préscolaire:
 « On demande à des élèves du préscolaire de répartir 27 objets dans 7 enveloppes de manière que chaque enveloppe n’en compte pas moins de 3 et pas plus de 5. On constate que les premières procédures observées sont très diverses. Certains élèves distribuent les objets un par un, d’autres mettent le maximum d’objets dans les premières enveloppes et d’autres encore répartissent les objets en tas de 3. Dans cet exemple, les élèves ne prennent pas explicitement en compte toutes les contraintes du problème, car, si tous les objets sont répartis, le bon nombre d’enveloppes ou le bon nombre d’objets par enveloppe ne sont pas toujours respectés.
« On demande à des élèves du préscolaire de répartir 27 objets dans 7 enveloppes de manière que chaque enveloppe n’en compte pas moins de 3 et pas plus de 5. On constate que les premières procédures observées sont très diverses. Certains élèves distribuent les objets un par un, d’autres mettent le maximum d’objets dans les premières enveloppes et d’autres encore répartissent les objets en tas de 3. Dans cet exemple, les élèves ne prennent pas explicitement en compte toutes les contraintes du problème, car, si tous les objets sont répartis, le bon nombre d’enveloppes ou le bon nombre d’objets par enveloppe ne sont pas toujours respectés.
C’est donc dire que, lorsque les élèves tentent une procédure, par exemple, mettre le maximum d’objets permis, soit cinq, dans les premières enveloppes, ils se rendent compte que cela ne fonctionne pas. Pour deux enveloppes, la contrainte de contenir minimalement 3 objets n’est pas respectée. »
La séquence d’apprentissage en trois temps que suppose l’enseignement-apprentissage PAR la résolution de problèmes prépare les élèves à la compréhension
Rôles dans une séquence d’apprentissage en trois temps
| Enseignant | Élève | |
| 1. Explorer |
Confie à l’élève la responsabilité et le pouvoir de résoudre la situation Observe et répond aux questions de clarification Questionne et propose des ajustements |
S’engage dans l’analyse et la compréhension: questionner, estimer, représenter Établit des relations entre les données Mobilise des concepts, des processus et des stratégies Active ses connaissances antérieures
|
| 2. S’engager |
Joue le rôle de médiateur Invite à communiquer en utilisant du vocabulaire mathématique Provoque une confrontation saine d’idées |
Propose des solutions en interaction avec ses pairs Compare Remet en question |
| 3. Conclure |
Rend explicite les apprentissages mathématiques Donne une rétroaction |
Se positionne face au développement de sa compréhension des concepts et des stratégies Consigne les conclusions |
Apprendre la mathématique POUR résoudre des problèmes
Au Québec, apprendre les mathématiques POUR résoudre des problèmes est présent dans les programmes depuis le début du 20e siècle comme en fait état un certain Monseigneur Ross en 1919: » L’enseignement est déjà pratique s’il s’exerce sur le concret (. . .) il faut le rendre plus pratique encore par le choix des problèmes toujours en rapport avec la vie réelle de l’élève. Il faut avoir soin de lui donner des notions exactes sur les poids en cours, les prix courants des objets, les quantités nécessaires à l’opération qui fait l’objet du problème. »
Apprendre la mathématique POUR résoudre des problèmes, tel que décrit dans le PFEQ, ne pourrait se limiter à la réalisation d’exerciseurs puisque le chemin à parcourir pour proposer une solution ne doit pas être déterminer d’emblée. Les enseignants ayant reçu la formation Résoudre et raisonner, comment mieux corriger? se souviendront de l’exemple de La terrasse (4e année).
Les épreuves proposées par le MEES, de par leur nature, sont des exemples de ce type d’intention
Résoudre des problèmes POUR apprendre à résoudre
« En tant que processus, la résolution de situations-problèmes constitue un objet d’apprentissage en soi. » PFEQ
Avoir comme intention l’enseignement et l’apprentissage de stratégies, c’est prendre le temps de planifier les situations choisies qui viendront enrichir le répertoire personnel des élèves. L’engagement dans un défi ne se trouve pas dans la complication d’une situation par de trop nombreuses étapes exigées à l’élève. La notion de situation complexe a peut-être fait son chemin dans notre désir de compréhension voulant distinguer la compétence Résoudre de la compétence Raisonner.
 Dans cette capsule, une enseignante pilote une situation-problème. Que peut-on remarquer? Pour le besoin, l’enseignante y joue un rôle. Les élèves, tant qu’à eux, sont plongés dans une situation habituelle ne leur permettant pas de deviner la mise en scène. Sommes-nous des metteurs en scène? Biscuits-lecture
Dans cette capsule, une enseignante pilote une situation-problème. Que peut-on remarquer? Pour le besoin, l’enseignante y joue un rôle. Les élèves, tant qu’à eux, sont plongés dans une situation habituelle ne leur permettant pas de deviner la mise en scène. Sommes-nous des metteurs en scène? Biscuits-lecture
Observons un exemple issu de la trousse du ministère pour des élèves de 3e année.

Pour inciter la réflexion et les échanges mathématiques tout en éveillant la curiosité et l’intérêt de l’élève, comment pourrait-on transformer cette situation.
En s’intéressant aux stratégies cognitives et métacognitives, cette situation pourrait être présentée selon l’Heuristique de résolution de problèmes de Pólya (1945) :
- Intention faisant appel au vécu des élèves: La semaine dernière, Sarah nous a proposé d’organiser un souper spaghetti pour ramasser les sommes nécessaires au déplacement en autobus vers la résidence de personnes âgées.
- Comprendre le problème et concevoir un plan: Sarah a apporté deux recettes: une à la viande pour 20 portions et une végétarienne pour 15 portions. Un élève propose d’utiliser une stratégie pour se représenter la situation choisie: Organiser un souper spaghetti.
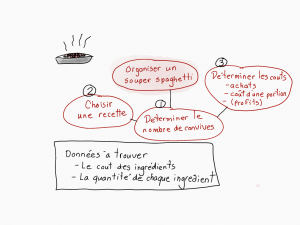 Ensemble, ils discutent des grandes étapes anticipées pour l’organisation de ce souper. Une autre stratégie est identifiée: trouver des données nécessaires à la réalisation des étapes.
Ensemble, ils discutent des grandes étapes anticipées pour l’organisation de ce souper. Une autre stratégie est identifiée: trouver des données nécessaires à la réalisation des étapes. - Mettre le plan à exécution
- Vérifier l’exactitude de la solution: Comme la situation est authentique, les élèves s’investiront d’avantage dans cette recherche d’exactitude.
Cet exemple propose donc de faire la liste des stratégies utilisées pour réaliser la situation en impliquant d’avantage les élèves. La référence à ces stratégies pour la réalisation de futures situations pourrait développer le sentiment de compétence des élèves. Au final, les étapes qui suivent, exigées par son auteur, s’imposeront d’elles-mêmes dans une dynamique d’engagement et d’accueil des idées mathématiques des élèves sans ce sentiment de complexité observé trop souvent dans l’offre de situations faite aux élèves.
- À la page suivante, choisis la sauce à spaghetti que tu préfères.
- Trouve, dans des circulaires de supermarchés, tous les ingrédients nécessaires à la préparation de cette sauce à spaghetti.
- Découpe les ingrédients et colle-les sur une feuille, ou écris simplement leurs noms.
- Trouve et écris le prix de chacun des ingrédients.
- N’oublie pas d’ajouter des pâtes à ta liste d’achats.
- Détermine le coût total des achats pour la préparation de ta sauce à spaghetti.
En temps de planification, il vous serait possible de choisir une situation existante pour la rendre plus près du vécu des élèves et répondre à l’une des trois intentions. Ainsi, l’élève se laissera convaincre de l’importance de se développer un répertoire de stratégies réellement aidantes afin de résoudre des problèmes POUR apprendre à résoudre des problèmes.






