Mettre l’accent sur le raisonnement spatial (lire la ressource en ligne ICI)
Le raisonnement spatial peut impliquer:
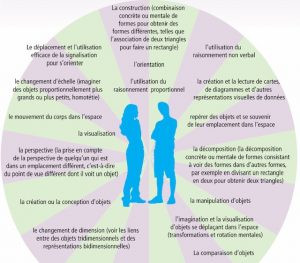
Bien qu’il soit important que le matériel de manipulation soit mis à la disposition des élèves, un aspect
encore plus essentiel est comment les utiliser de façon pertinente et efficace, c’est-à-dire en tant que partie
intégrante de la pensée spatiale et de la résolution de problèmes. Autrement dit, la tâche d’apprentissage
est conçue de façon à ce que le matériel de manipulation ne soit pas uniquement utilisé pour communiquer
ou montrer des représentations de la pensée après le travail cognitif de la résolution du problème; ce
sont les outils servant à résoudre le problème.
Numération et sens du nombre : La droite numérique peut être un outil efficace pour développer
le sens du nombre chez les élèves. Lorsque l’on explore les nombres entiers ou les nombres rationnels
avec les élèves, une droite constitue une représentation visuo-spatiale efficace des quantités et de leurs
diverses relations.
Mesure : Les activités de mesure offrent de nombreuses occasions d’apprentissage qui font appel à la
pensée spatiale.
Géométrie et le sens de l’espace : La géométrie et le sens de l’espace peuvent être développés et
améliorés grâce à des casse-têtes et des jeux. Dès les premières années d’études et tout au long de leur
parcours scolaire, les casse-têtes offrent aux élèves de vastes possibilités d’exercer leurs habiletés de
pensée spatiale. Les tangrams et les pentominos sont deux exemples dans lesquels des pièces se prêtent
à des jeux et des activités de type casse-tête, qui permettent de développer des habiletés telles que la
composition ou la décomposition de formes, l’exploration des transformations géométriques (réflexions,
transformations, rotations), la visualisation et la congruence.
Modélisation et algèbre : L’exploration et l’observation de régularités dès la maternelle
requièrent un raisonnement à la fois arithmétique et visuo-spatial.
Jeux et activités ludiques: Un grand nombre d’activités ludiques supposent une pensée spatiale. C’est le cas des casse-têtes, de nombreux jeux de table, des jeux guidés avec des blocs ou d’autres formes géométriques, et de certains
types de jeux vidéo. Selon de nombreuses recherches, des liens ont été établis entre ces types d’activités
ludiques et le raisonnement spatial, et aussi, dans certains cas, les résultats en mathématiques (voir
Tepylo, Moss et Hawes, 2014).
Représentations graphiques : Des représentations graphiques de toutes sortes nous permettent de
créer des représentations visuelles de données. Au cours des années du primaire, il s’agit de diagrammes
concrets, de pictogrammes et de diagrammes à bandes. Nous pouvons aussi représenter graphiquement
des expressions algébriques pour mettre en évidence des suites non numériques à motif croissant. Les
graphiques nous permettent de voir l’aspect ou la nature de nos données et d’étudier les changements
et les tendances de croissance.
 Selon le triangle de Jean Houssaye, la didactique met en relation l’enseignant et les savoirs (enseigner). Selon J. Houssaye, l’élève risque d’être oublié par un enseignement trop théorique. Par la pédagogie, l’enseignant participe à la formation de l’élève. On parlera d’apprentissage lorsque l’élève sera en relation avec les savoirs. Comme on le voit, l’enseignant est à l’aise avec le rôle d’observateur des apprentissages de l’élève si les fondements pédagogiques et didactiques sont présents. Ainsi, questionner la didactique est essentiel.
Selon le triangle de Jean Houssaye, la didactique met en relation l’enseignant et les savoirs (enseigner). Selon J. Houssaye, l’élève risque d’être oublié par un enseignement trop théorique. Par la pédagogie, l’enseignant participe à la formation de l’élève. On parlera d’apprentissage lorsque l’élève sera en relation avec les savoirs. Comme on le voit, l’enseignant est à l’aise avec le rôle d’observateur des apprentissages de l’élève si les fondements pédagogiques et didactiques sont présents. Ainsi, questionner la didactique est essentiel. 
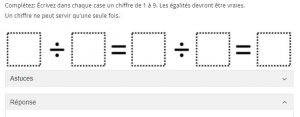
 QUESTIONS DE LA SEMAINE
QUESTIONS DE LA SEMAINE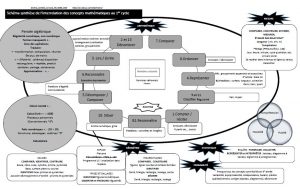

 En commençant par la généreuse ressource
En commençant par la généreuse ressource  Le Nombre tout bien réfléchi présente toutes ces ressources sur un mur Padlet à clôner pour votre utilisation personnalisée. Onglet RESSOURCES /Développer la pensée mathématique / Activités mathématiques et routines savoir
Le Nombre tout bien réfléchi présente toutes ces ressources sur un mur Padlet à clôner pour votre utilisation personnalisée. Onglet RESSOURCES /Développer la pensée mathématique / Activités mathématiques et routines savoir


 Avec l’arrivée des réseaux sociaux, une multitude de ressources s’adresse à l’enseignante et à l’enseignant. L’interprétation que se font les auteurs des ensembles didactiques ou du matériel complémentaire ne se substitue pas à l’interprétation que se donne l’enseignante ou l’enseignant dans l’exercice de son jugement professionnel.
Avec l’arrivée des réseaux sociaux, une multitude de ressources s’adresse à l’enseignante et à l’enseignant. L’interprétation que se font les auteurs des ensembles didactiques ou du matériel complémentaire ne se substitue pas à l’interprétation que se donne l’enseignante ou l’enseignant dans l’exercice de son jugement professionnel.  L’Appui du mardi s’intéresse aux idées mathématiques des élèves. Comment les motiver?
L’Appui du mardi s’intéresse aux idées mathématiques des élèves. Comment les motiver?