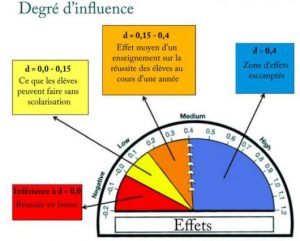
 John Hattie1 a fait des recherches sur plus de 800 méta-analyses qui résument plus que 50000 études individuelles. .
John Hattie1 a fait des recherches sur plus de 800 méta-analyses qui résument plus que 50000 études individuelles. .
Selon le classement2, la zone d’effets escomptés se situe au-delà de 0,4 .
Voici quelques facteurs qui pourraient influencer la réussite en mathématique.
Pour en savoir plus: Le monde est notre classe, la classe est notre monde.
Les élèves qui pensent à haute voix (effet de taille : 0,98)
Les programmes piagétiens (effet de taille : 0,73)
Fournir une rétroaction (effet de taille : 0,71)
Des pratiques d’enseignement explicites (instruction directe) (effet de taille : 0,65)
L’apprentissage assisté par un pair (effet de taille : 0,62)
L’enseignement de la résolution de problèmes (effet de taille 0,60)
Sources:
- Normand, Romuald. Enseignement des mathématiques: ce qui marche selon John Hattie, 2018
- Baromètre de Hattie
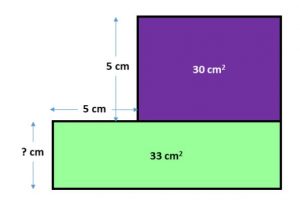

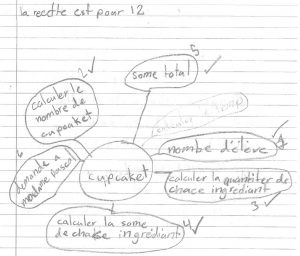

 Selon les travaux réalisés par Nathalie Bisaillon, Université de Montréal, pour la soutenance de sa thèse en novembre 2021 : Développement du sens du nombre et de la numération : élaboration d’un outil d’évaluation et d’une séquence didactique, certaines difficultés des élèves québécois semblent persister depuis les travaux de Nadine Bednarz et Bernadette Dufour-Janvier réalisés en 1986. Bien que le sens du nombre soit un prédicteur important de la réussite scolaire, madame Bisaillon fait le constat que les conditions à mettre en place pour favoriser son développement n’occupent pas une assez grande place dans l’enseignement actuel de l’arithmétique.
Selon les travaux réalisés par Nathalie Bisaillon, Université de Montréal, pour la soutenance de sa thèse en novembre 2021 : Développement du sens du nombre et de la numération : élaboration d’un outil d’évaluation et d’une séquence didactique, certaines difficultés des élèves québécois semblent persister depuis les travaux de Nadine Bednarz et Bernadette Dufour-Janvier réalisés en 1986. Bien que le sens du nombre soit un prédicteur important de la réussite scolaire, madame Bisaillon fait le constat que les conditions à mettre en place pour favoriser son développement n’occupent pas une assez grande place dans l’enseignement actuel de l’arithmétique. 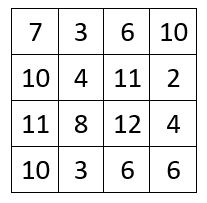
 John Hattie1 a fait des recherches sur plus de 800 méta-analyses qui résument plus que 50000 études individuelles. .
John Hattie1 a fait des recherches sur plus de 800 méta-analyses qui résument plus que 50000 études individuelles. .  « Dans les premières années du primaire, à travers les livres d’histoires, il est possible de se pencher sur la notion du temps et de questionner les élèves sur leur conception à cet égard. On peut ainsi faire réaliser aux élèves que les unités de temps peuvent être très petites (secondes) ou très grandes
« Dans les premières années du primaire, à travers les livres d’histoires, il est possible de se pencher sur la notion du temps et de questionner les élèves sur leur conception à cet égard. On peut ainsi faire réaliser aux élèves que les unités de temps peuvent être très petites (secondes) ou très grandes
 « Les chercheurs privilégient une approche de l’enseignement des mathématiques par la résolution de problèmes, car elle encourage les élèves à développer et approfondir leur compréhension tandis qu’ils développent des justifications les aidant à résoudre la tâche qui leur a été confiée. Dans une classe constructiviste, écrit Marian Small, les élèves sont
« Les chercheurs privilégient une approche de l’enseignement des mathématiques par la résolution de problèmes, car elle encourage les élèves à développer et approfondir leur compréhension tandis qu’ils développent des justifications les aidant à résoudre la tâche qui leur a été confiée. Dans une classe constructiviste, écrit Marian Small, les élèves sont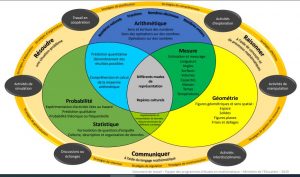 Voir la formation offerte par le ministère en décembre 2020:
Voir la formation offerte par le ministère en décembre 2020: 


