Le saucissonnage qui tue le sens: un mot de madame Stella Baruk: ICI

1. Qu’est-ce qu’un bon problème?

Les situations-problèmes  proposées à l’élèves dans le cadre de l’enseignement-apprentissage de la mathématique devraient faire l’objet d’une analyse à priori.  Selon Charnay (2003), un bon problème doit permettre d’atteindre la zone proximale de la majorité des élèves. L’enseignant doit donc documenter son choix en émettant des hypothèses sur:  

• les démarches, les stratégies et les procédures que les élèves utiliseront;
• les obstacles qu’il rencontreront et les erreurs que ceux-ci engendreront;
• l’organisation pédagogique qui favorisera l’apprentissage dans la classe;
• les interventions à mettre en place qui favoriseront l’apprentissage. 

Les caractéristiques d’un problème selon le Référentiel d’intervention en mathématique (RIM, 2019) : 

• il est formulé clairement sous forme d’un énoncé écrit, oral ou même illustré, de façon à être compris par tous les élèves;
• il est énoncé de façon à ne pas induire une stratégie de résolution ou l’emploi d’un algorithme en particulier;
• il éveille la curiosité et maintient l’intérêt des élèves;
• il incite à la réflexion et aux échanges mathématiques;
• il est à la portée de tous les élèves tout en leur offrant un défi;
• il se prête à l’utilisation d’une variété de stratégies de résolution;
• il fait appel au vécu des élèves;
• il donne lieu à une ou plusieurs réponses correctes.

Grille d’analyse a priori d’un bon problème

**************************************

Lire la suite

Le géocaching est une activité agréable à faire avec les élèves de tous âges ou les membres de sa famille et ses amis.  Il faut un téléphone intelligent et un accès gratuit au site geocaching.com

Lire la suite

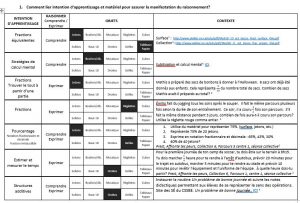
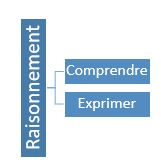
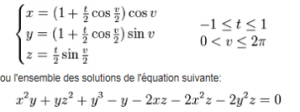Comprendre et exprimer son raisonnement avec flexibilité et fluidité

Version PDF de cet article

Inspiré du Référentiel d’intervention en mathématique et éclairé par les données récentes de la recherche, cet article aborde le sujet du matériel de manipulation.

1. Quels sont les différents modes de représentation qui supportent le raisonnement mathématique de mes élèves?

Selon le Référentiel d’intervention en mathématique, l’élève s’engage cognitivement dans l’activité mathématique ou y participe activement lorsqu’il communique en appuyant ses propos à l’aide de modes de représentation ou en les combinant pour expliciter sa pensée mathématique. À cet égard, le MEQ (2006) précise que les élèves communiquent en mathématique en utilisant les différents modes de représentation suivants :

• mots;
• symboles et expressions numériques;
• dessins ou schémas, diagrammes et figures;
• grilles et tableaux;
• matériel de manipulation.

Modes de représentation en mathématique ( PFEQ, enseignement secondaire, p.124)

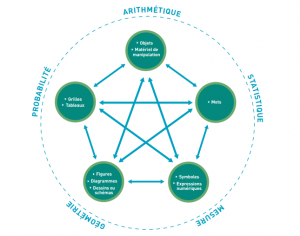
Ces différents modes de représentation peuvent être utilisés par l’élève et par l’enseignant, de façon isolée ou combinés entre eux, afin de donner du sens à un ou à des concepts et processus ou encore de soutenir des propos lors du partage d’un raisonnement à l’oral ou à l’écrit. Il est important que l’élève se montre flexible dans le passage d’un mode de représentation à un autre (NCTM, 2000; Pape et Tchoshanov, 2001). En effet, comme le précise Duval (2007), chaque mode de représentation est incomplet en soi pour ce qui est de permettre, de comprendre et d’exprimer un raisonnement. En ce sens, une juxtaposition ou une articulation des modes de représentation est souhaitable et permet d’approfondir la compréhension conceptuelle et de soutenir la communication ainsi que le raisonnement.

2. Est-ce que le matériel de manipulation produit à lui seul l’apprentissage?

Le matériel de manipulation est un mode de représentation pour lequel certaines précisions doivent être apportées. En effet, l’utilisation du matériel de manipulation pour favoriser l’apprentissage de la mathématique est soutenue par des données probantes provenant de méta-analyses (Carbonneau, Marley et Selig, 2013; Jitendra, Nelson, Pulles, Kiss et Houseworth, 2016). Cependant, le fait que les élèves aient en leur possession du matériel de manipulation ne produira pas à lui seul un apprentissage. Il faut également que l’enseignant ait une intention d’apprentissage claire dont la prise en considération sera facilitée par ce matériel.

Utiliser le matériel de manipulation, une activité mathématique en soi.^{2 et 3}

Dans une perspective où les mathématiques se constituent en contexte, peu importe le contexte, faire des mathématiques avec du matériel ne serait pas une version concrète de ce que c’est de faire des mathématiques sans matériel, mais une activité mathématique en soi. Ainsi, il est important de mettre en évidence l’apport du matériel lors de l’analyse a priori d’une tâche mathématique.

La routine au service du développement de la compréhension du sens du nombre

Le nombre tout bien réfléchi est un tableau virtuel (Padlet) permettant aux élèves d’émettre leurs idées mathématiques liées à l’arithmétique.   Selon la Progression des apprentissages, les concepts et les processus à acquérir et à maîtriser dans le champ de l’arithmétique constituent la base en mathématique, puisqu’ils sont réinvestis dans tous les autres champs de la discipline.  Dans un contexte de développement de la numératie, il importe de reconnaître les relations qui existent entre ces différents apprentissages essentiels du champ de l’arithmétique qui devraient être durables, préalables et transférables.

Cette routine du nombre du jour invite donc les élèves à manifester une pensée mathématique flexible pour exprimer leurs idées, si besoin, avec du matériel.  Par exemple, avec le nombre 23,03 , les élèves pourraient utiliser la corde à linge ou une droite numérique pour affirmer que 23,3 est plus grand que 23,03 ou que 23,03 = 23  et 3/100. 

3. Quels sont les avantages, pour les élèves et l’enseignant, à utiliser du matériel de manipulation?⁵

Lorsque les élèves utilisent du matériel de manipulation, on les encourage à essayer différentes approches et à prendre des risques leur permettant de trouver eux-mêmes les réponses. On les invite à explorer et à représenter des concepts mathématiques de diverses façons à l’aide d’outils d’apprentissage concrets. Cela augmente la quantité d’information sensorielle qu’ils acquièrent et les aide à se rappeler les procédés mathématiques à utiliser pour résoudre de futurs problèmes (Garforth et Siegel, 2014). ⁴

Avantages pour les élèves

• Approfondir leur compréhension des concepts mathématiques abstraits.
• Créer un répertoire d’images auquel se référer lorsque les symboles abstraits deviennent trop complexes.
• Résoudre des problèmes.
• Représenter la pensée mathématique.
• Développer des stratégies cognitives et métacognitives.

Avantages pour l’enseignant

• Multiplier les occasions d’observer les élèves en action.
• Offrir de la rétroaction immédiate.
• Réguler son enseignement.
• Permettre de donner du « sens » aux différents objets à manipuler.

Ressources pour l’inspiration de contextes signifiants

• Atelier.on.ca 
• Charbonneau, Caroline. (2019) La manipulation en mathématique au cœur des apprentissages. Chenelière Éducation.
• Prest, Séance collective, accès gratuit pour les enseignants du CSSBE.
• Site des services éducatifs du CSSBE : L’armoire math interactive (web), Le matériel de manipulation, Subitisation et boulier rekenrek, Un problème de bonne journée, Fluidité, flexibilité et calcul mental, etc.  

Un mot à propos des épreuves du ministère 2022

Lors des examens du ministère, les élèves de 6^e peuvent utiliser du matériel de manipulation pour réaliser les tâches de compétences Résoudre (C1) et Raisonner (C2). C’est dans le guide d’administration que l’on retrouve la liste du matériel autorisé (édition 2019).

Il est à noter que pour l’évaluation de la compétence Résoudre (C1), le lexique est interdit en 2022.  Ainsi, il devient important de planifier aux séquences d’apprentissage du temps pour consigner les observations à propos des concepts et processus.  Cette consignation devra se faire sur un document recto-verso de dimension lettre.  Vous pouvez visiter le site des services éducatifs à ce sujet.

Avant de commencer

Il serait intéressant de proposer à vos élèves du 3^e cycle les deux activités suivantes pour le permettre de réfléchir à la stratégie :  Utiliser le matériel de manipulation.

• Le ruban de Möbius

1. Observer la capsule vidéo : https://youtu.be/SosdtAc-72Q
2. Remettre une bande de papier à chaque élève dans le but de fabriquer le ruban de Möbius.
3. Recueillir les observations des élèves en leur posant la question suivante :

Le ruban de Möbius est un objet à manipuler qui révèle certains concepts mathématiques.  À lui seul, te permet-il de comprendre? 

Au besoin, pour des élèves curieux, présenter la formule mathématique complexe associée au ruban. Est-ce que le ruban a révélé ses secrets mathématiques? Les mathématiciens qui ont révélé les formules savantes, ont-ils eu besoin de manipuler le ruban?  Le vocabulaire et les symboles mathématiques sont-ils  importants pour exprimer le raisonnement?

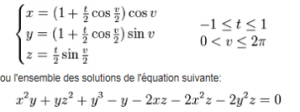
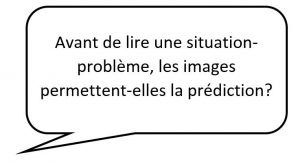
Invitez les élèves à préciser leur perception du matériel de manipulation mathématique. À quel moment pourrait-il être utile pour comprendre ou expliquer?  À quelles conditions le matériel de manipulation devient-il mathématique?  Le matériel de manipulation est-il réservé aux élèves du premier cycle? 

À la suite de cette discussion, il serait intéressant de préciser la gestion du matériel dans votre classe.  En commençant par identifier un lieu, comme une étagère dans la classe, ou le matériel serait rangé .

• Le casse-tête de Desjardins et Hétu en trois temps

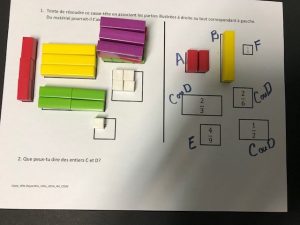
Temps 1 ACTIVER: Remettre l’Annexe A aux élèves. Leur demander de décrire ce qui est présenté et de préciser de qui est attendu.  Quelles sont les connaissances nécessaires pour relever le défi? Du matériel de manipulation pourrait-il nous aider (réglettes)?

Temps 2 EXPLORER: Observer les élèves qui explorent la situation et manifestent leur raisonnement. Au besoin, engager la conversation mathématique en questionnant.  

Que peux-tu dire des entiers C et D?  Pourquoi sais-tu que cette réglette représente la moitié?

Temps 3 EXPRIMER: Animer un temps d’échanges pour que les élèves expriment leur raisonnement en identifiant les obstacles rencontrés ou les certitudes.

Terminer l’activité en invitant les élèves à identifier les avantages à utiliser la stratégie. Ajouter à l’aide-mémoire de classe et personnel les découvertes réalisées.

Voir des élèves du 3e cycle raisonner à l’aide du casse-tête de Desjardins et Hétu. 

• Je développe mon raisonnement du concept de fraction à l’aide de blocs mosaïques

Raisonnement fractions_mosaique_3e cycle_exemples élèves

Raisonnement fractions_mosaique_3e cycle

Voir des élèves du 3e cycle  en action.

*****************************

1. Ministère de l’éducation (2019). Référentiel d’intervention en mathématique.
2. Corriveau et Jeannotte (2015). L’utilisation de matériel en classe de mathématique au primaire : quelques réflexions sur les apports possibles
3. Corriveau et Jeannotte (2019). Le matériel de manipulation : ça va de soi que ça ne va pas de soi
4. TA à l’école (2020). Utilisation de matériel de manipulation pour appuyer l’apprentissage des mathématiques à la maison
5. Les maths : quoi de 9? Qu’entend-on par « matériel de manipulation » ?

Voici le support visuel de la section A du questionnaire pour chacune des épreuves mathématiques de 2e et 4e années.