Résoudre une situation-problème 1 L’objectif des tâches pour évaluer la compétence Résoudre une situation-problème mathématique n’étant pas de mesurer la maitrise des algorithmes, la calculatrice peut généralement être autorisée. En cours d’année, c’est l’enseignant qui décide, selon la complexité de la tâche et la grandeur des nombres en jeu, de permettre ou non l’utilisation de …
Catégorie : Concepts
Fév 08
Résolution de problèmes au secondaire
Tout comme au primaire, les enseignants.es du secondaire ont à développer les compétences suivantes: Résoudre une situation-problème (30%) Déployer un raisonnement mathématique (70%) Communiquer à l’aide du langage mathématique En 2021, plusieurs enseignants.es du primaire et du secondaire ont été initiés au Référentiel d’intervention en mathématique (RIM) et ont ajouté à leurs choix pédagogiques trois …
Jan 26
Questions-réponses mathématiques
L’enseignement des mathématiques peut parfois questionner. Vous trouverez ici des questions souvent posées. QUESTIONS DE LA SEMAINE Quels sont les concepts et processus susceptibles d’être mobilisés dans les épreuves obligatoires de mathématique de 6e année de l’année scolaire 2021-2022? Voir la page 10 du Document d’information 022-610 ICI. Enseignants-es de 6e année, où en est l’aide-mémoire de …
Jan 07
Open middle ou Problème du milieu
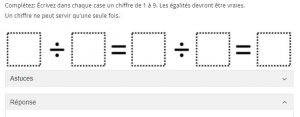
Un Open middle ou Problème du milieu invite les élèves à considérer une variété d’inconnus. Ainsi, leur pensée mathématique gagne de la flexibilité ce qui évite le développement d’un contrat didactique qui leur fait considérer le symbole = comme un donneur de réponses. Exemple: Accéder au site Open Middle ICI.
Jan 07
Menseki pour raisonner les concepts de mesure
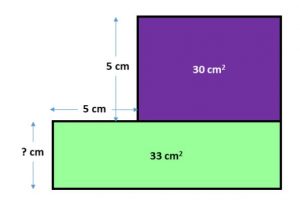
Les Menseki sont des casse-tête japonais qui contribuent au développement du raisonnement mathématique. Un casse-tête peut être proposé en routine pour nos élèves du 3e cycle afin de les encourager à manifester une pensée mathématique flexible et fluide pour la compréhension des concepts de mesure (longueur et aire). Exemple: On trouve les Menseki Version internet …
Nov 19
Sens du nombre et groupement
Selon les travaux réalisés par Nathalie Bisaillon, Université de Montréal, pour la soutenance de sa thèse en novembre 2021 : Développement du sens du nombre et de la numération : élaboration d’un outil d’évaluation et d’une séquence didactique, certaines difficultés des élèves québécois semblent persister depuis les travaux de Nadine Bednarz et Bernadette Dufour-Janvier réalisés en 1986. …
Nov 01
L’heure: aspect ordinal et aspect cardinal
« Dans les premières années du primaire, à travers les livres d’histoires, il est possible de se pencher sur la notion du temps et de questionner les élèves sur leur conception à cet égard. On peut ainsi faire réaliser aux élèves que les unités de temps peuvent être très petites (secondes) ou très grandes(années). Ces unités …
Oct 21
Le dénombrement
Retrouver l’article complet sur le site TaÀlÉcole: Qu’est-ce que le dénombrement? Number talk, un site pour développer les stratégies de dénombrement.
Août 25
Littératie, numératie : à vous de jouer!
Jouer, c’est prendre des risques! Rajotte, AQEP (2019), p. 14 « Le gout du risque que permet la mise en œuvre d’uneapproche, basée sur la pédagogie par le jeu, s’avère un avantage indéniable pour développer la compréhension de l’élèvede l’addition et de la soustraction (Marinova, 2016a). En effet,cette pratique pédagogique se traduit par le « paradoxe …
Juin 23
Développer la pensée logique
Une pensée mathématique flexible suppose aussi une pensée logique. Plusieurs jeux permettent de développer cette pensée. On peut également profiter des routines. Faire verbaliser l’élève sur ses idées mathématiques aide à développer la pensée. En contexte de résolution de problèmes, avoir accès à la pensée des camarades contribuent au développement de la pensée de chaque …