Compte déplacé par le centre d'identité (2013-08-15 11:06:56)
Articles de cet auteur
Juil 05
Développer le raisonnement spatial
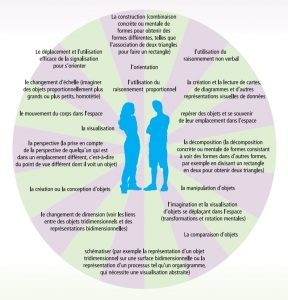
Mettre l’accent sur le raisonnement spatial (lire la ressource en ligne ICI) Le raisonnement spatial peut impliquer: Bien qu’il soit important que le matériel de manipulation soit mis à la disposition des élèves, un aspectencore plus essentiel est comment les utiliser de façon pertinente et efficace, c’est-à-dire en tant que partieintégrante de la pensée spatiale …
Avr 26
Apprendre et évaluer autrement en mathématique
Le contenu de ce site est le fruit de la collaboration entre le RÉCIT MST et plusieurs conseillers pédagogiques en mathématique, conseillers pédagogiques du RÉCIT et professionnels de l’éducation afin de proposer des solutions concrètes pour apprendre et évaluer les compétences et les apprentissages mathématiques. Rejoindre la ressource ICI.
Mar 29
Utilisation de la calculatrice au primaire
Résoudre une situation-problème 1 L’objectif des tâches pour évaluer la compétence Résoudre une situation-problème mathématique n’étant pas de mesurer la maitrise des algorithmes, la calculatrice peut généralement être autorisée. En cours d’année, c’est l’enseignant qui décide, selon la complexité de la tâche et la grandeur des nombres en jeu, de permettre ou non l’utilisation de …
Mar 14
Le voyage extraordinaire de l’Endurance (littérature)
En mars 2022, l’Endurance est retrouvé dans l’Antarctique plus de 100 ans après son naufrage. La lecture de l’album jeunesse L’aventure vraie d’Ernest Shackleton est une belle occasion de développer les nombreux éléments de numératie qu’offre la littérature jeunesse, mais également de construire une ligne du temps pour suivre le déroulement de l’expédition entre 1914 et …
Fév 24
Matériel didactique: approuvé ou conforme?
Autonomie professionnelle Avec l’arrivée des réseaux sociaux, une multitude de ressources s’adresse à l’enseignante et à l’enseignant. L’interprétation que se font les auteurs des ensembles didactiques ou du matériel complémentaire ne se substitue pas à l’interprétation que se donne l’enseignante ou l’enseignant dans l’exercice de son jugement professionnel. Ainsi, une ressource, bien que créée avec …
Fév 08
Résolution de problèmes au secondaire
Tout comme au primaire, les enseignants.es du secondaire ont à développer les compétences suivantes: Résoudre une situation-problème (30%) Déployer un raisonnement mathématique (70%) Communiquer à l’aide du langage mathématique En 2021, plusieurs enseignants.es du primaire et du secondaire ont été initiés au Référentiel d’intervention en mathématique (RIM) et ont ajouté à leurs choix pédagogiques trois …
Fév 02
Développer les idées mathématiques (Appui mardi)
L’Appui du mardi s’intéresse aux idées mathématiques des élèves. Comment les motiver? Analyse a priori d’une situation-problème. 1er cycle, Élève 1er cycle 2e cycle 3e cycle, Élève 3e cycle 2. Des …
Jan 26
Questions-réponses mathématiques
L’enseignement des mathématiques peut parfois questionner. Vous trouverez ici des questions souvent posées. QUESTIONS DE LA SEMAINE Quels sont les concepts et processus susceptibles d’être mobilisés dans les épreuves obligatoires de mathématique de 6e année de l’année scolaire 2021-2022? Voir la page 10 du Document d’information 022-610 ICI. Enseignants-es de 6e année, où en est l’aide-mémoire de …
Jan 07
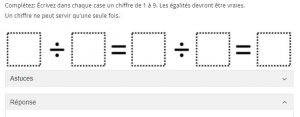
Open middle ou Problème du milieu
Un Open middle ou Problème du milieu invite les élèves à considérer une variété d’inconnus. Ainsi, leur pensée mathématique gagne de la flexibilité ce qui évite le développement d’un contrat didactique qui leur fait considérer le symbole = comme un donneur de réponses. Exemple: Accéder au site Open Middle ICI.
Jan 07
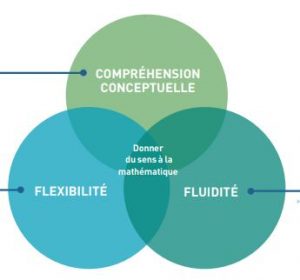
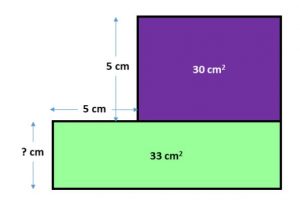
Menseki pour raisonner les concepts de mesure
Les Menseki sont des casse-tête japonais qui contribuent au développement du raisonnement mathématique. Un casse-tête peut être proposé en routine pour nos élèves du 3e cycle afin de les encourager à manifester une pensée mathématique flexible et fluide pour la compréhension des concepts de mesure (longueur et aire). Exemple: On trouve les Menseki Version internet …