Les compétences Résoudre et Raisonner ont principalement un statut d’action cognitive1. Rappelons-nous que, selon le PFEQ, la distinction entre les deux compétences est essentiellement une question d’accent mis sur différentes facettes de l’exercice de la pensée mathématique où tout s’intègre. Dans ce contexte, l’enseignant.e choisit la résolution de problèmes pour développer cette pensée mathématique et assurer la compréhension conceptuelle, la flexibilité et la fluidité.
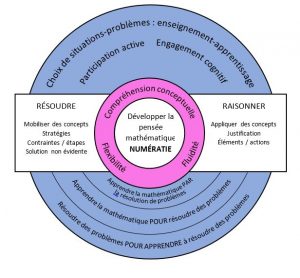
Observons le casse-tête de Desjardins et Hétu (1974).

Dans cette situation, l’enseignant pourrait avoir comme intention d’apprentissage les composantes Décoder et Valider de la compétence à résoudre ou encore la composante Justifier des actions de la compétence à raisonner. Ici, on fait appel à la compréhension et à la pensée fluide de l’élève qui doit associer une fraction à une partie d’un tout. Que pourrait-il dire à propos de 1/2 et 4/8 ? Est-ce la représentation de la même surface dans le casse-tête? Pourquoi?
Ainsi, pour une même tâche, qui correspond aux conditions énoncés par le programme, il est possible de développer ou d’évaluer la compétence 1 et/ou la compétence 2.
- Selon le pilotage de la tâche: pour apprendre à résoudre ou pour résoudre par exemple.
- Selon le moment dans la séquence d’enseignement: le moment où l’élève réalise la tâche peut avoir un effet direct sur les caractéristiques de cette tâche et peut faire en sorte que l’on puisse développer ou évaluer la compétence 1 ou la compétence 2.
- Selon les composantes et les critères: pour chaque tâche, une ou des composantes sont sélectionnées dans la compétence choisie et des critères d’évaluation sont ciblés.
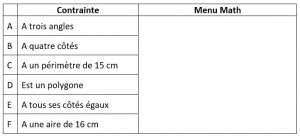
Voici un exemple avec une tâche du Menu math .
| Résoudre (C1) | Raisonner (C2) |
|
|
|
Madame Josée utilise une tâche du Menu math pour inviter les élèves à considérer plusieurs contraintes leur permettant de mobiliser les concepts qu’ils connaissent. L’élève fera plusieurs allers-retours pour valider la tâche en utilisant des stratégies variées. Par triangulation de l’évaluation, madame Josée souhaite observer ses élèves au moment où il mobilisent leurs connaissances et voir de quelle façon ils valident leur processus. Les traces laissées par les élèves –production- aideront madame Josée à apprécier les différentes stratégies de communication de la solution. Par conversation, elle rencontrera 3 élèves pour apprécier les traces laissées sur le support papier. |
Madame Josée utilise la tâche du Menu math pour vérifier s’ils savent appliquer les différents concepts de géométrie et de mesure.
Par triangulation de l’évaluation, madame Josée souhaite converser avec deux élèves ciblés pour apprécier leur raisonnement mathématique. De plus, lors de la présentation en grand groupe, elle jugera de la justesse des traces laissées –production– sur le support papier par les élèves ayant pris la parole pour justifier leur solution. |
Accompagner en trois temps les élèves en difficulté
Lors du choix de situations-problèmes, il est important d’identifier les obstacles mathématiques anticipés. Ainsi, les interventions didactiques pourraient être élaborées, lors de la phase de préparation, avec l’ensemble du groupe ou avec certains élèves qui éprouvent des difficultés.
- Temps 1: Phase de préparation pour rencontrer les élèves en difficulté en sous-groupes. Leur faire vivre une activité mathématique en privilégiant la manipulation d’objets réels impliqués dans la situation-problème à vivre prochainement (par exemple, manipuler des livres à placer dans un boîte pour réfléchir à la notion de volume) ou demander à ces élèves de représenter cette situation à l’aide de dessins.
- Temps 2: Phase de préparation et de réalisation de la situation-problème avec l’ensemble des élèves.
- Temps 3: En quelques minutes, vivre la phase d’intégration en sous-groupes avec les élèves en difficulté.
Aller plus loin: Formation en ligne du ministère: Pistes d’action visant une mise en oeuvre réaliste et harmonisée des programmes d’études en mathématique, novembre 2020.
Triangulation_MenuMath_Exemple de planification_CSSBE_mars2021
Planification_preuvesApprentissage_CSSBE_mars2021 (canevas)
Exemples de consignation:
1. MenuMaths_liste_eleves_preuves apprentissage
2.
–