Résolution de problèmes au secondaire

Tout comme au primaire, les enseignants.es du secondaire ont à développer les compétences suivantes:

• Résoudre une situation-problème (30%)
• Déployer un raisonnement mathématique (70%)
• Communiquer à l’aide du langage mathématique

En 2021, plusieurs enseignants.es du primaire et du secondaire ont été initiés au Référentiel d’intervention en mathématique  (RIM) et ont ajouté à leurs choix pédagogiques trois intentions:

Si on ouvre la PDA du secondaire en mathématique, le premier paragraphe présente l’élève du primaire.  Voici ce qu’un.e enseignant.e peut y lire:

« Dès le primaire, les élèves sont placés dans des situations d’apprentissage qui leur permettent d’utiliser des objets, du matériel de manipulation, des ouvrages de référence ainsi que des outils ou des instruments. Les activités et les tâches qui leur sont proposées les amènent à réfléchir, à manipuler, à explorer, à construire, à simuler, à discuter, etc. Les élèves peuvent ainsi s’approprier des concepts, des processus et des stratégies utiles à la mathématique. Ils doivent également faire appel à leur intuition, à leur sens de l’observation, à leurs habiletés manuelles de même qu’à leur capacité de s’exprimer, de réfléchir et d’analyser. Ils apprennent ainsi à établir des liens, à se représenter des objets mathématiques de différentes façons et à les organiser mentalement pour en arriver progressivement à l’abstraction. Graduellement, les élèves développent un ensemble de connaissances et d’habiletés mathématiques qu’ils apprennent à maîtriser et à utiliser efficacement afin d’être fonctionnels dans la société. » page 5

Au secondaire: 

« …les apprentissages se poursuivent dans le même esprit. Ils s’articulent autour des préoccupations sousjacentes à l’activité mathématique : interpréter le réel, généraliser, anticiper, prendre des décisions. Ces préoccupations renvoient aux grandes questions qui ont conduit l’homme à construire la culture et les savoirs mathématiques au fil du temps. Elles sont donc porteuses de sens et soutiennent la construction par les élèves de boîtes à outils pour communiquer adéquatement dans ce langage qu’est la mathématique, pour raisonner efficacement en établissant des liens entre tous les concepts et les processus mathématiques et, enfin, pour résoudre des situations- problèmes. Une importance est accordée aux outils technologiques, qui favorisent l’émergence et la compréhension de concepts et de processus mathématiques tout en augmentant l’efficacité des élèves dans le traitement de situations diverses. L’utilisation pertinente de concepts mathématiques et de stratégies variées leur permet d’appréhender efficacement divers sujets de la vie quotidienne. Associées aux activités d’apprentissage, certaines situations qu’ils vivent au quotidien soutiennent le développement de savoir-faire et de savoir-agir mathématiques qui leur permettent de mobiliser et de consolider leurs connaissances mathématiques et d’en acquérir de nouvelles. Au deuxième cycle, les élèves approfondissent leur pensée mathématique, essentielle à la poursuite d’études plus avancées. »

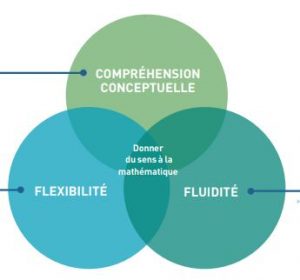
Comme on peut le constater, au primaire comme au secondaire, on se soucie de donner du sens à la mathématique en encourageant une pensée mathématique faisant preuve de compréhension, de fluidité et de flexibilité.  

Donner du sens à la mathématique par l’interrelation

entre la compréhension conceptuelle, la flexibilité et la fluidité. (RIM, page 11)

Quelques conseils d’une enseignante d’expérience de première secondaire:

• L’utilisation de situations-problèmes doit mettre l’élève devant des obstacles mathématiques non pas compliqués, mais complexes. Ainsi, en s’assurant de proposer des situations respectant la zone proximale de  développement des élèves, on évite l’expression de dégoût que certains manifestent dès le mois de septembre. 
• Je propose des situations ayant le moins de lecture possible.  J’évite les situations dont la lecture ou le contexte représentent un obstacle.
• Dans l’organisation de mon horaire, je choisis des situations-problèmes qui se réaliseront le temps d’une période à mon horaire, soit une heure. 
• J’utilise souvent l’intention d’apprendre la mathématique pour résoudre des problèmes.  Ainsi, la planification de mes cours commence par l’enseignement ou la découverte de concepts qui seront appliqués ou mobilisés dans des situations-problèmes.  
• En septembre, les élèves ont souvent de la difficulté à organiser leurs traces.  Je les encourage à numéroter les étapes de leur démarche. 
• Question langage mathématique, je dois parfois défaire les traces de calculs ne respectant pas la barre d’équivalence dans un algorithme debout ou le symbole = dans une équation.  Ainsi, 14 +5= 19 + 3 = 22 devient 14 + 5 = 19   et 19 + 3 = 22 ou 14 + 5 + 3 = 22.