La lecture des problèmes présentés sous la forme écrite demande à l’élève la construction d’une représentation mentale aidant la compréhension (Goulet, Voyer 2014). Ainsi, compréhension de texte informatif et habileté à répondre à des questions d’inférence sont des facteurs motivant la réussite en mathématique.
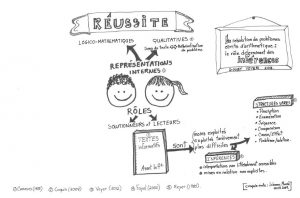
Les œuvres littéraires et documentaires présentées au bas de cet article offrent de nombreuses possibilités d’exploitation mathématique. Certaines ciblent un contenu spécifiquement mathématique –les albums à compter par exemple- alors que d’autres se laissent découvrir avec un regard attentif comme celui que porte Loma sur la littérature jeunesse. Ainsi, il est possible de fixer une intention mathématique de lecture tout en s’intéressant aux idées mathématiques émises par les élèves lors de la lecture d’œuvres littéraires et documentaires.
L’exploitation de la littérature jeunesse est un merveilleux véhicule permettant de développer la numératie et la culture mathématique. Par ses symboles, ses représentations et ses codes particuliers, la numératie couvre l’ensemble des connaissances et des habiletés permettant à une personne d’être fonctionnelle en société. L’élève doit ainsi être accompagné pour en reconnaître la présence dans son environnement et dans les œuvres littéraires et documentaires qu’il découvre.
Textes informatifs
« Pour diverses raisons, la compréhension des textes informatifs exige une coordination de connaissances, d’habiletés et de stratégies de la part des lecteurs. Tout d’abord, ils présentent des structures variées, peu connues des élèves (Murphy, 2013; Fayol, 2016; Williams et Pao, 2013). De plus, ils portent sur des sujets souvent éloignés du vécu des jeunes et proposent un vocabulaire spécifique. Sans compter que la compréhension de ces textes demande aux lecteurs de faire de nombreuses inférences, c’est-à-dire de faire des liens entre une information lue et leurs connaissances ou encore entre deux informations du texte non liées explicitement. Moins les sujets sont familiers, plus l’inférence est difficile à faire.
Pour toutes ces raisons, les textes informatifs sont considérés comme étant plus exigeants sur le plan cognitif que d’autres types d’écrits, par exemple les récits (Dockrell, Connelly, Walter et Critten, 2015). Toutes ces spécificités font en sorte que les enseignants se sentent parfois démunis lorsque vient le temps de les enseigner, ne sachant trop par où commencer. Les textes informatifs, bien qu’ils soient présents
dans toutes les disciplines scolaires, font donc peu l’objet d’un enseignement planifié et spécifique. Puisqu’ils sont moins exploités directement en classe, les lecteurs peinent à les comprendre. » (ADEL, 2019)
Lecture interactive
« Apprendre à lire, c’est d’abord et avant tout apprendre à comprendre. Trop souvent, au dire de Tauveron (2001), on propose aux élèves des textes lisses, où il n’y a rien à comprendre, rien à explorer.
« La lecture interactive est un dialogue entre l’adulte et l’élève autour d’un récit qui se fait en cours de lecture à voix haute. Il s’agit d’un contexte d’apprentissage social et interactif où l’adulte joue un rôle de médiateur auprès de l’élève. L’intervention en lecture interactive permet de suivre de près le développement des élèves en intensifiant le niveau de difficulté, entre autres, par le choix des livres et des questions posées. Bien que l’élève n’ait pas à traduire lui-même le code, l’ensemble des processus est visé par l’intervention où l’adulte, par le questionnement, amène l’élève à lier causalement les éléments du récit dans le but d’assurer la compréhension et la cohésion » (La lecture interactive: questionner l’élève pour mobiliser les processus en lecture, Vivre le primaire, 2016)
Ce dialogue entre l’enseignant et les élèves peut parfois être teinté d’une intention mathématique. La planification de la lecture interactive permet à l’enseignant de prévoir quelques ouvertures: un élément déclencheur inspirant les stratégies de résolution d’un problème; des illustrations permettant d’inférer que le personnage principal aime les mathématiques ou la présence de certains concepts (ordre croissant, régularités, figures géométriques, etc); la description d’un lieu permettant de dresser le plan d’une pièce ou d’un quartier pour se repérer; un sentiment particulier face aux mathématiques manifesté par un personnage; la présence de symboles mathématiques; l’estimation du temps que dure le récit ou la longueur d’un parcours; la référence à un illustre mathématicien ou une illustre mathématicienne; etc.
La lecture interactive selon Alexandra Hontoy
|
Ce qu’est la lecture interactive.
|
Ce que la lecture interactive n’est pas.
|
Ressources
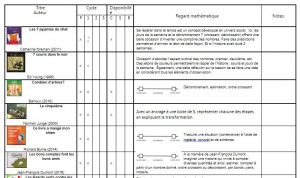Regard mathématique sur la littérature jeunesse: plusieurs oeuvres littéraires et documentaires accompagnées de suggestions pour une exploitation mathématique.
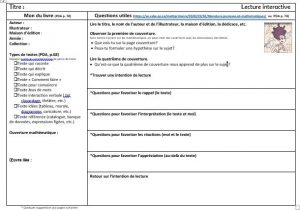Lecture interactive: planification d’une lecture interactive à l’aide d’un album de votre choix. Plusieurs suggestions de questions pour soutenir le développement des quatre dimensions (Compréhension, interprétation, réaction et appréciation)
Suggestions des participants au Bivouac littératie numératie (document collaboratif).
Ressources en ligne et suggestions d’exploitation mathématique
|
752 lapins François Blais et Valérie Boivin (2016)
Livre audio ICI (6 minutes)
|
1er cycle Dans cette histoire, le 752e lapin d’une gentille princesse se sauve. Comment le retrouver?
|
|
Tu n’es pas (si) petit! Anna Kang, Christopher Weyant (2017)
Extrait: ICI |
Préscolaire et 1er cycle Des ours se rencontrent. Mais qui donc est petit? Qui donc est grand? Belle introduction à la comparaison et invitation au dialogue sur la différence. À la suite de l’histoire, utiliser des blocs emboîtables pour raconter l’histoire en misant sur la comparaison (plus petit, plus grand). |
|
La tour Eiffel a des ailes Mymi Doinet et Aurélien Débat (2009)
Cette sculpture se trouve à St-Georges. Imagine qu’elle voyage…
|
1er cycle et petits curieux ou curieuses du 2e cycle La littérature jeunesse permet de voyager! La tour Eiffel s’ennuie et s’évade pour découvrir la France. L’écoute de la lecture, enrichie des illustrations, permet d’attirer l’attention sur quelques données chiffrées: son poids, sa taille en unités non conventionnelles.
|
|
La girafe pas de cou Carole Tremblay (2020)
En apprendre plus sur les girafes avec Kirikou
|
1er et 2e cycle Porter un regard mathématique sur la littérature jeunesse avec l’album La girafe pas de cou -disponible dans Samuel- a intéressé des élèves de la maternelle à la 4e année. En prime, une belle réflexion sur la différence. À la suite de la lecture, les élèves ont représenté l’histoire à l’aide de bandes de carton. Bien sûr notre Girafe Gertrude a fait l’objet d’une comparaison. Les élèves de 2e cycle ont voulu comparer la hauteur de Gertrude avec d’autres animaux à l’aide de nombres décimaux. L’occasion était belle de sortir un documentaire pour choisir de nouvelles données chiffrées. La représentation a également donné l’idée de rechercher des équivalences. Les idées mathématiques des élèves sont riches! Au passage, le vocabulaire s’est enrichi: les ossicônes n’ont plus de secret pour ces élèves! |
|
Cendrillon Squeletton Robert SanSouci (2007)
Version de Charles Perrault Sur le site de la Bibliothèque et Archives nationales du Québec ICI , inscris Cendrillon dans le moteur de recherche. Version audio. |
2e et 3e cycle Tu connais certainement l’histoire de Cendrillon imaginée par Charles Perrault. L’auteur s’amuse à la transformer: Cendrillon vit dans un cimetière. Et voilà une proposition plutôt morbide…
|
|
Émile Pantalon Mireille Levert (2005)
Sur le site de la Bibliothèque et Archives nationales du Québec ICI , inscris Émile dans le moteur de recherche. Version audio. |
1er cycle Émile Pantalon est grand, très grand, trop grand.
|
|
Les yeux noirs (1999)
|
1er et 2e cycle Mathieu est non voyant. Se repérer dans l’espace requiert des stratégies particulières. Quelles sont-elles? Imaginer un parcours et demander à un camarade ayant les yeux bandés d’y circuler en suivant les consignes: à gauche , avance de 3 pas, etc. Les mathématiques, c’est une question d’image mentale. Écouter l’histoire en imaginant les illustrations et la relire ou la regarder avec les illustrations pour inviter les élèves à discuter de l’importance des représentations. |
|
Les contes qui comptent
|
1er cycle L’application donne accès à des histoires proposant des idées mathématiques. L’enfant peut écouter l’histoire, s’enregistrer pour lire ou s’enregistrer pour émettre une idée mathématique. Un lecteur choisi par l’élève pourrait également enregistrer sa voix. |
Documents joints
This work by johanne.morin is licensed under a Creative Commons Attribution-NonCommercial 4.0 International
