Sens du nombre et groupement

Selon les travaux réalisés par Nathalie Bisaillon, Université de Montréal,  pour la soutenance de sa thèse en novembre 2021 : Développement du sens du nombre et de la numération : élaboration d’un outil d’évaluation et d’une séquence didactique, certaines difficultés des élèves québécois semblent persister depuis les travaux de Nadine Bednarz et Bernadette Dufour-Janvier réalisés en 1986.  Bien que le sens du nombre soit un prédicteur important de la réussite scolaire, madame Bisaillon fait le constat que les conditions à mettre en place pour favoriser son développement n’occupent pas une assez grande place dans l’enseignement actuel de l’arithmétique. 

Bednarz et Dufour-Janvier¹ affirment : Par numération, on entend généralement un système cohérent de symboles régi par certaines règles (regroupement par 10, valeur positionnelle, etc.) permettant d’écrire les nombres, de les lire. La numération est la partie de l’arithmétique qui enseigne à exprimer et à représenter les nombres. Ainsi dans l’enseignement actuel, la numération est souvent identifiée à  la capacité de lire des nombres, de les écrire et à l’habileté de pointer, dans un nombre donné,  les valeurs de position (valeurs associée à chacun des chiffres dans cette écriture dépendant de sa position). On retrouve alors un enseignement axé essentiellement sur l’écriture conventionnelle et sur l’acquisition des règles syntaxiques qui régissent cette  écriture, et ceci très tôt (dès la 1^re année, 6-7 ans).  »

• Conception de l’écriture « séquence de chiffres »

Pour les besoins de leur recherche, Bednarz et Dufour-Janvier ont demandé aux élèves de 8 à 10 ans d’utiliser des étiquettes groupements pour tenter de trouver le nombre mystère 445 (que l’enseignant garde secret et que l’élève doit découvrir) se situant entre 402 et 513.  (Voir Annexe 1  : Interprétation de la valeur de position en termes de groupements.)  Pour plus du quart des élèves, l’écriture des nombres est vu comme un alignement de chiffres, les enfants ne prennent alors pas du tout en considération les mots centaines, dizaines, unités écrits sur les étiquettes.

L’alignement systématique proposé par les tableaux de numération contribuent à cette conception. On se rappelle que la PDA propose d’utiliser le tableau de numération uniquement à partir de la 2^e année.  Imposer prématurément  une représentation ordonnée conduit nécessairement  l’enfant à une interprétation de l’écriture en termes de découpage , d’ordre, et écarte toute signification véritable accordée à la position en termes de groupements.

Obstacle à la production de nouvelles connaissances : les décimaux

Plus tard, dans le parcours scolaire, avec les apprentissages associés aux nombres décimaux, cette conception peut inciter les élèves à identifier 2,19 le nombre obtenu si on ajoute 1 dixième à 2,9 . Cette interprétation est donc un prolongement direct de la conception séquence de chiffres.  

Multiplication par 10, 100, 1000

Cette conception qui incite l’élève à considérer la séquence de chiffres est également observée lorsqu’une opération demande de multiplier par 10 et que le truc demandant d’ajoute un zéro est introduit trop tôt.  Des erreurs du type 5,13 x 10 = 5,130 sont alors observées.

L’importance du zéro

Quatre chiffres sont proposés à l’élève sur des étiquettes;  2,5,5 et 3.  On demande à l’élève de former un nombre à 4 chiffres. Par la suite, on demande aux élèves d’ajouter le 0 pour former un nombre plus grand.  Le raisonnement de l’élève qui affirme que le zéro devant ne change rien et que le 0 à la suite augmente la valeur pourrait encore ici brouiller la compréhension des nombres décimaux.  7,390 deviendra alors plus grand que 7,39  ou 5,039 sera égal à 5,39.

• Conception collection de l’écriture des nombres

La présentation d’un ensemble de traits, comme illustré à droite,  pourrait permettre de constater 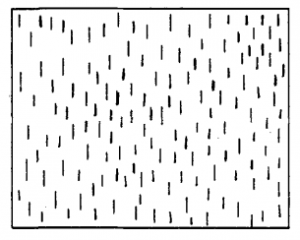la conception collection plutôt que groupements.  L’élève qui dénombre 1 à 1 ou qui utilise  des groupements uniquement pour compter plus vite par 10 démontre une compréhension inachevée de l’écriture du nombre qui découle directement des groupements. Avec notre exemple, 14 groupes de 10 et 7 traits devraient être traduit par 147 sans avoir besoin de compter par bonds de 10 : 10-20-30-40-50 etc.

Encore ici, la conception du nombre peut venir assombrir la compréhension des opérations.  Demander à des élèves de représenter le nombre 3152 sur un abaque et d’y enlever 128 pourrait révéler une certaine incompréhension associée aux groupements. Et que se produit-il parfois avec l’algorithme : 3152 – 128 ? Certains élèves n’ont-ils pas le réflexe de faire 8 – 2 unités puisque, diront-ils- 2 – 8 n’est pas possible…

Planifier les interventions

Comme le dit si bien Michel Lyons dans Les incontournables du nombre, l’enseignant ou l’enseignante qui s’assoit dans le cerveau de l’élève s’insère dans sa pensée mathématique pour mieux planifier ses interventions.

1. https://www.researchgate.net/publication/225565972_Une_etude_des_conceptions_inappropriees_developpees_par_les_enfants_dans_l’apprentissage_de_la_numeration_au_primaire