 Un problème de bonne journée, 80 situations pour travailler le sens des opérations. PDF Word
Un problème de bonne journée, 80 situations pour travailler le sens des opérations. PDF Word
Le piège des mots clés-clés
Les chercheurs et les spécialistes en didactique des mathématiques émettent depuis longtemps des mises en garde contre la méthode consistant à attirer l’attention des élèves sur certains mots-clés (de plus, de moins, somme, différence, etc.) se retrouvant dans des situations-problèmes par lesquels on voudrait obtenir le sens des opérations.
Les élèves meilleurs au préscolaire et en première année
Selon Lovin et Van de Walle p.90, de nombreux enfants du préscolaire et la plupart des élèves de première année réussissent mieux à résoudre des problèmes que les élèves de niveau supérieur. Les élèves plus âgés ne tiennent pas toujours compte du contexte et utilisent souvent des données superflues dans leurs calculs. En revanche, les élèves du préscolaire et de première année ont peu d’outils pour calculer voir aucun. Ils examinent donc attentivement le problème, emploie souvent des modes de représentation variés et déterminent la solution en s’appuyant sur le sens de l’histoire. Quel que soit le niveau auquel vous enseignez, il est important de toujours demander aux élèves de réfléchir aux problèmes avant de tenter de les résoudre.
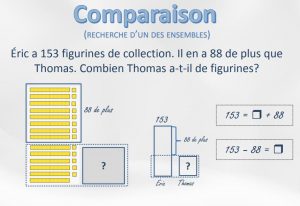
À titre d’exemple, le problème qui suit est réussi par uniquement 40% d’un groupe d’élèves de 8 ans : Raphaël possède 45 petites autos. Léonie possède 12 petites autos de moins que Raphaël. Combien Léonie a-t-elle de petites autos? La capsule de 1 minute intitulée Le piège montre un élève de 2e année traduisant cette situation par : 45 + 12 = 57 Sommes-nous étonnés? Quel serait le taux de réussite de ce second problème : Raphaël possède 45 petites autos. C’est 20 de plus que Léonie. Combien de petites autos possède Léonie?
Une ressource pour développer le sens des opérations au quotidien
Un problème de bonne journée , un recueil préparé par Nadia Roy ,enseignante de 2e cycle à l’école Ste-Famille de Tring Jonction, offre près de 80 courtes situations impliquant des structures additives (addition et soustraction) et des structures multiplicatives (multiplication et division). Chaque type de problème est précédé de conseils didactiques permettant à vos élèves de développer des représentations personnelles et variées qui manifesteront leur capacité de comprendre le sens des opérations. Ce développement didactique est inspiré des travaux d’Annie Savard de l’Université McGill. La formation Deux ours, un renard et le fromage est une formation CSSBE offerte aux enseignants qui désirent développer la représentation des structures additives à partir d’une histoire.
Proposées en routine quotidienne -dans l’ordre ou en variant les types de structures, avec ou sans données chiffrées- les différentes situations-problèmes permettent aux élèves du 2e cycle de raisonner avec justesse tout en développant la confiance en leurs idées mathématiques. Des représentations sont suggérées sans être imposées. Elles ont tout de même l’avantage d’être fort utiles lorsque les données chiffrées impliquent de grands nombres difficiles à représenter par des jetons.
Les différents sens à développer au primaire
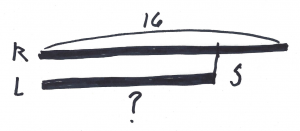
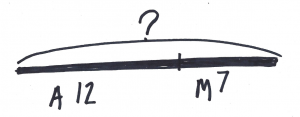
Sens de l’addition et de la soustraction (A. Savard et MÉQ) |
|
    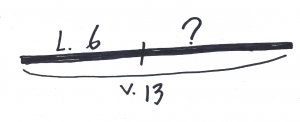  |
|
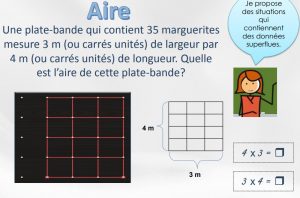
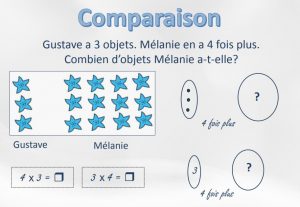
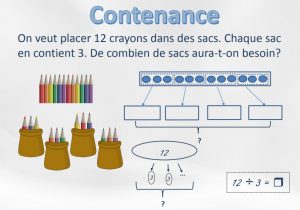
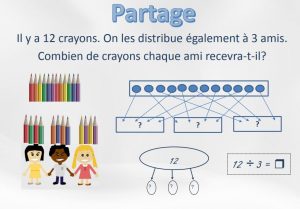
Sens de la multiplication et de la division (MÉQ) |
|
    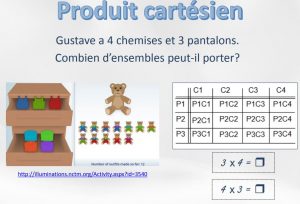  |
Formations CSSBE
 Deux oursons, un renard et le fromage, une histoire comme élément déclencheur
Deux oursons, un renard et le fromage, une histoire comme élément déclencheur
Ressources
 Sur le site du ministère : webinaire et documents d’accompagnement.
Sur le site du ministère : webinaire et documents d’accompagnement.
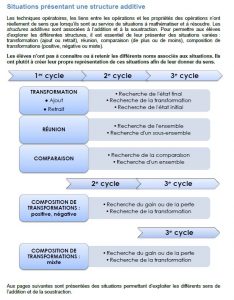
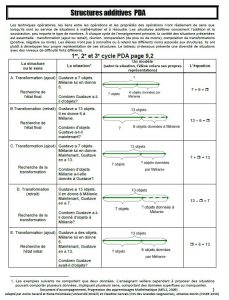 Représentations des différentes structures additives (modèle A. Savard)
Représentations des différentes structures additives (modèle A. Savard)







