Développer la pensée algébrique

Documents et activités: ICI

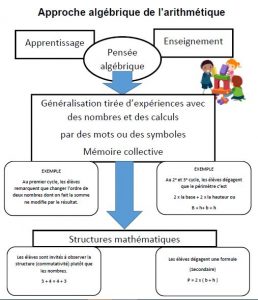
C’est quoi? Le raisonnement algébrique est présent dans tous les domaines mathématiques. Il consiste à décrire des régularités caractérisant des relations entre des quantités – contrairement à l’arithmétique, qui consiste à effectuer des calculs portant sur des quantités connues. En gros, le raisonnement algébrique concerne la généralisation d’idées mathématiques et l’identification de structures mathématiques.

Pourquoi? Le raisonnement algébrique sous-tend toute la pensée mathématique, y compris l’arithmétique, car il nous permet d’explorer la structure des mathématiques. Nous reconnaissons maintenant l’importance d’inclure le raisonnement algébrique dans l’enseignement des mathématiques dès un très jeune âge, afin de rendre accessibles à tous les élèves ces idées mathématiques très efficaces.

Nous avons tous la capacité de penser algébriquement, car le raisonnement algébrique constitue, essentiellement, la façon dont les humains interagissent avec le monde. Dans notre quotidien, nous recherchons des régularités, nous prêtons attention à des aspects importants de ces régularités, puis nous faisons des généralisations tirées de situations familières pour les appliquer à des situations peu familières. Le raisonnement algébrique est présent dans de nombreux aspects de nos vies; par exemple, faire des comparaisons pour trouver le fournisseur de téléphones cellulaires qui offre le meilleur contrat ou pour déterminer des temps et des distances lorsque nous conduisons.

Le élèves peuvent développer leur raisonnement algébrique de diverses façons :

• Exploration des propriétés, des relations et des fonctions

        Propriétés des nombres : nombres pairs, impairs, premiers, composés, divisibilité, etc.

        Effet des opérations sur ces nombres : propriétés des opérations

       Termes manquants (relation entre les opérations, opération inverse)

       Variables :  Euler

        Fonctions :  « Un de plus que  » est une relation fonctionnelle qui vaut pour tous les  nombres.  La règle qui associe un polygone avec le nombre de sommets

• Exploration de l’égalité en tant que relations entre les quantités 

         Le signe = indique une égalité et non pas le synonyme d’effectuer un calcul et inscrire la réponse après le symbole d’égalité :

                              Égalité  (quantité) 5 x 3 = 5 + 5 + 5    15 = 15

                              Équivalence (sens) 5 x 3 = 3+3+3+3+3

                              Expressions équivalentes : 52 = 40 +12      25 + 27 = 40 + 12    

• Utilisation des symboles algébriques comme variables

                    4 x ___ = 12    ___ = 3 

• Régularités : numériques et non numériques
• Modes de représentation (symbolique, numérique et graphique)